Funciones de Excel: Formato Condicional, BUSCARH, BUSCARV y Tabla Dinámica.

Excel como ya lo mencione anteriormente es muy útil para facilitar y automatizar el trabajo, estas funciones tienen muchas aplicaciones y te ayudan a ahorrar tiempo. En el siguiente documento encontrarás información acerca de estas cuatro funciones de Excel y ejemplos de sus aplicaciones. Espero que la información te sirva de ayuda.

Funciones de excel from Elisa Reyes

Excel y su uso para resolver problemas algebraicos.

Excel es un software que sirve para realizar cualquier tipo de operaciones matemáticas. En el siguiente documento se muestra un ejemplo muy básico del uso del Excel para resolver problemas algebraicos. Espero y te sea de utilidad.

¡Saludos!

Excel y su uso para resolver problemas algebraicos from Elisa Reyes

Actividad cuatro

En este documento contiene los temas de Conceptos algebraicos, términos semejantes, suma, multiplicación y división algebraica.

Actividad 4 contestada from Elisa Reyes

Día de muertos en México.

Te mostraré tres videos referentes al día de muertos y después de cada uno mi opinión personal del mensaje que intenta transmitir cada uno.

Este video fue hecho por estudiantes no mexicanos.

Creo que este video se muestra un concepto en el cual hay una vida después de la muerte, y que no debemos de ponernos tristes con la muerte de un ser querido; porque ellos ya no van a sufrir. En el video se muestra a una niña que acaba de perder a su madre y está triste; después ella es arrastrada hasta el fondo de la tumba, donde descubre un mundo nuevo y fascinante, lleno de alegría, de folclor,  de vida. En este mundo podemos observar las costumbres y tradiciones mexicanas, como su gastronomía, su música entre otras. Al darse cuenta la niña que su madre estaba en un mundo tan maravilloso ya no se sintió triste, recordó a su madre con una sonrisa en lugar de recordarla con un lagrima.

El segundo vídeo también fue elaborado por estudiantes, pero esta vez, de México se titula: "De un jalón hasta el panteón" y fue elaborado por:

Trabajo final de la carrera de Diseño de la Comunicación Gráfica en la UAM X.
Neomi David, David Herrera y Enrique Sañudo.

Este video fue mi favorito de los tres pues creo que se muestra la verdadera intención u objetivo del día de muertos, el cual es recordar a nuestros familiares y amigos que ya no están entre nosotros,  recodar los momentos que compartimos con ellos, las cosas buenas que no dieron y/o enseñaron y honrar su memoria. También se muestra la apatía  que se puede dar  en algunas personas que desconocen que es el día de muertos o cuál es su intención. Como  mexicanos hay que honrar, respetar y festejar nuestras tradiciones, sentirnos orgullosos de nuestra cultura. Y trasmitirla de generación en generación. Pienso que el video es muy conmovedor, te hace reflexionar  y te deja una enseñanza. También me pareció increíble el trabajo de los estudiantes Mexicanos que lo crearon, pues hicieron un gran trabajo.

Por último un vídeo hecho por profesionales titulado "Hasta los huesos"

Una producción de: Instituto Mexicano de Cinematografía / Calavera Films / Roberto Rochín / San Pedro Post / ITESO; con el apoyo de Cinema W / Universidad de Guadalajara / FONCA / Virgin Studios / New Art / La Curva / Secretaría de Educación Pública / Lotería Nacional / Grupo Modelo

El tercer  y último video  tiene unos efectos padrísimos. Pienso que el mensaje fue que se tiene  un miedo sin fundamento a la muerte se tiene miedo a lo que vendrá después de ella, cuando no hay nada que temer. El video te muestra como el protagonista está asustado y no acepta que esté muerto, se niega a creerlo.  Pero al ver que  no le va a pasar nada malo y que no tiene nada que temer se tranquiliza y acepta la muerte.  También en el video se muestra a la catrina que es el símbolo de esta maravillosa tradición mexicana.

Creo que los tres videos tienen una cosa en común, la cual es la alegría. En los tres se muestra unos lugares felices llenos de magia y donde las costumbre mexicanas se conservan aún después de la muerte.

¡El álgebra, la herramienta más útil de la vida!

El álgebra es una de las ramas matemáticas de gran importancia y que dio la pauta al desarrollo de las ciencias como la física, química, entre otras.  Su uso está en nuestra vida diaria, nos ayuda a simplificar muchos trabajos y cuentas que usamos diariamente.

En el mundo laboral es utilizada por los profesionales que van desde los electricistas, los arquitectos,  los informáticos e ingenieros.  Algunos autores definen al algebra como la puerta de entrada hacia el éxito en el siglo XXI. Puesto que todo profesional capacitado debe dominar esta área matemática y aplicarla a su profesión. A continuación conoceremos lo orígenes del álgebra.

¿Qué es el álgebra?

Conocer y entender bien el concepto nos ayuda a facilitar su comprensión; a continuación  se muestran 4 definiciones de cuatro autores diferentes.

      1° Definición: Es la rama de la matemática que estudia la combinación de elementos de estructuras abstractas acorde a ciertas reglas.

      2° Definición: Algebra es el nombre que identifica a una rama de la Matemática que emplea números, letras y signos  para poder hacer referencia a múltiples operaciones aritméticas.

      3° Definición: Generalización de la aritmética que en lugar de emplear números concretos, se representan las cantidades mediante símbolos.

      4° Definición: Parte de las matemáticas que estudia las operaciones en las que hay cantidades conocidas en las que se representan con números y otras desconocidas representadas por letras.

Todas estas definiciones resultan un tanto complicadas de entender y no son del todo correctas. Entonces ¿Qué es el álgebra?

“El álgebra es un lenguaje; como todo lenguaje  tiene sus propias reglas, su sintaxis (la forma en que se debe de escribir un lenguaje) y la forma en que se lee dicho lenguaje”

Este lenguaje es precisamente el utilizado para expresar cualquier disciplina científica he ahí la importancia del álgebra.

Historia del álgebra

Etimología:

La palabra álgebra viene del árabe al-gabr, que significa poco más o menos ‘la recomposición o recolocación de los trozos de una cosa que se ha roto.

Etapas del álgebra:

Los periodos o etapas del álgebra se divide en:

a)    “álgebra retórica”: no existen abreviaturas, ni símbolos especiales. Se usa el mismo lenguaje escrito. Época paleobabilónica entre 2000 y 1600 a. n. e.

b)    “álgebra sincopada”: este término lo ideó Nesselman en 1842. Se usan ya algunos términos algunos términos técnicos y abreviaturas. Ejemplo la Aritmética de Diofanto. Siglo III.

c)    “álgebra simbólica”: Es ya un álgebra mucho más parecida a la que usamos hoy. Con símbolos especiales, incógnitas, etc.. Siglos XVI y XVII, Vièta.

El origen del álgebra puede rastrearse en Babilonia y en Egipto hace unos 4000 años, ya que, se han encontrado una serie de escritos antiguos de estas civilizaciones, donde se describe la forma de resolver ecuaciones, los escritos más importantes que se han encontrado son: Papiro de Rhind, Los Elementos de Euclides y Los nueve capítulos sobre el arte matemático.

El álgebra en las civilizaciones antiguas

El álgebra en la antigua Babilonia:

La principal fuente de información sobre la civilización y la matemática babilónica procede de textos grabados con inscripciones cuneiformes en tablillas de arcilla. Los textos se escribían sobre las tablillas cuando la arcilla estaba aún fresca. Después podían borrarse y usarse otra vez o también cocerse en hornos o simplemente se endurecían al sol. Las tablillas más antiguas que se conservan son del 2000 a.C. Varios miles de tablillas esperan todavía ser descifradas.

Estas tablillas han proporcionado abundante información sobre el sistema numérico y los métodos de cálculo que usaban. También las hay con textos que contienen problemas algebraicos y geométricos. Los babilonios disponían de fórmulas para resolver ecuaciones cuadráticas. No conocían los números negativos por lo que no se tenían en cuenta las raíces negativas de las ecuaciones. Su sistema de numeración era de base 60 y ha llegado hasta nosotros en la medida del tiempo y de los ángulos. Llegaron a resolver problemas concretos que conducían a sistemas de cinco ecuaciones con cinco incógnitas e incluso se conoce un problema astronómico que conduce a un sistema de diez ecuaciones con diez incógnitas. Tampoco conocían el cero lo que lleva a problemas de interpretación de las cantidades. Para evitar el problema, reducían el tamaño de las cifras adyacentes. A partir del siglo VI a.C. Sin embargo, fue utilizado un signo de omisión interior, es decir una especie de cero.

Por supuesto en esta fase el álgebra es retórica, es decir no se usan símbolos especiales. Si aparecen palabras como por ejemplo su  (longitud) usadas como incógnitas posiblemente porque muchos problemas algebraicos surgen de situaciones geométricas y esto hizo que esa terminología se impusiera. También usaban antiguos pictogramas sumerios para designar las incógnitas de una ecuación.

El álgebra en la civilización egipcia:

Dejaron pocas evidencias matemáticas. El papiro es un material que resiste mal el paso del tiempo. Hay dos papiros de gran importancia: el papiro Rhind y el Moscú. El Rhind fue confeccionado hacia 1650 a.C. por un escriba llamado Ahmes quien dice haberlo copiado de un original doscientos años más antiguo. Expone 87 problemas y sus soluciones y se usa la escritura hierática en vez de la jeroglífica. No se sabe si fue escrito al estilo de un libro de texto el cuaderno de notas de un alumno. El Moscú es parecido con 25 problemas y sus soluciones. En lo referente al álgebra, los papiros contienen soluciones a problemas con una incógnita. Sin embargo los procesos eran puramente aritméticos y no constituían un tema distinto a éste que es el predominante junto con problemas geométricos.

El álgebra en la civilización china:

De la época de la primera dinastía Han (206 a. C. hasta 24 d.C.) procede el tratado Matemáticas en nueve Libros. Posteriormente otros matemáticos como Liu Hui (siglo III), Sun-zi (siglos II-IV), Liu Zhuo (siglo VI) y otros hicieron aportaciones a este tratado. El texto trata problemas económicos y administrativos como medición de campos, construcción de canales, cálculo de impuestos,..Trabajan las ecuaciones lineales indeterminadas y un procedimiento algorítmico para resolver sistemas lineales parecido al que hoy conocemos como método de Gauss que les llevó al reconocimiento de los números negativos. Estos números constituyen uno de los principales descubrimientos de la matemática china. La escuela algebraica china alcanza su apogeo en el siglo XIII con los trabajos de Quin Jiu-shao, Li Ye, Yang Hui y Zhu Shi-jie que idearon un procedimiento para la resolución de ecuaciones de grado superior llamado método del elemento celeste o tian-yuanshu. Este método actualmente se conoce como método de Horner, matemático que vivió medio milenio más tarde. El desarrollo del álgebra en esta época es grandioso: sistemas de ecuaciones no lineales, sumas de sucesiones finitas, utilización del cero, triángulo de Tartaglia ( o Pascal) y coeficientes binomiales así como métodos de interpolación que desarrollaron en unión de una potente astronomía. El siglo VII vió la enorme gesta de ingeniería que supuso la unión de los dos ríos más importantes de China mediante el Gran Canal de 1700 km. de largo.

El álgebra en la civilización india:

Son muy escasos los documentos de tipo matemático que han llegado a nuestras manos, pese a tener constancia del alto nivel cultural de esta civilización. Aun más que en el caso de China, existe una tremenda falta de continuidad en la tradición matemática hindú y al igual que ocurría con las tres civilizaciones anteriores, no existe ningún tipo de formalismo teórico. Los primeros indicios matemáticos se calculan hacia los siglos VIII-VII a.C, centrándose en aplicaciones geométricas para la construcción de edificios religiosos y también parece evidente que desde tiempos remotos utilizaron un sistema de numeración posicional y decimal. Fue, sin embargo, entre los siglos V-XII d.C cuando la contribución a la evolución de las matemáticas se hizo especialmente interesante, destacando cuatro nombres propios: Aryabhata (s.VI), Brahmagupta (s.VI), Mahavira (s. IX) y Bhaskara Akaria (s.XII). La característica principal del desarrollo matemático en esta cultura, es el predominio de las reglas aritméticas de cálculo, destacando la correcta utilización de los números negativos y la introducción del cero, llegando incluso a aceptar como números validos las números irracionales. Profundizaron en la obtención de reglas de resolución de ecuaciones lineales y cuadráticas, en las cuales las raíces negativas eran interpretadas como deudas. Desarrollaron también, sin duda para resolver problemas astronómicos, métodos de resolución de ecuaciones diofánticas, llegando incluso a plantear y resolver (siglo XII) la ecuación x²=1+ay², denominada ecuación de Pelt. Como resumen acabaremos diciendo que en la historia de la India se encuentran suficientes hechos que ponen en evidencia la existencia de relaciones políticas y económicas con los estados griegos, egipcios, árabes y con China. Matemáticamente se considera indiscutible la procedencia hindú del sistema de numeración decimal y las reglas de cálculo.

Edad Moderna:

Durante la Edad Moderna europea tienen lugar numerosas innovaciones, y se alcanzan resultados que claramente superan los resultados obtenidos por los matemáticos árabes, persas, indios o griegos. Parte de este estímulo viene del estudio de las ecuaciones polinómicas de tercer y cuarto grado. Las soluciones para ecuaciones polinómicas de segundo grado ya era conocida por los matemáticos babilónicos cuyos resultados se difundieron por todo el mundo antiguo.

El descubrimiento del procedimiento para encontrar soluciones algebraicas de tercer y cuarto orden se dieron en la Italia del siglo XVI. También es notable que la noción de determinante fue descubierta por el matemático japonés Kowa Seki en el siglo XVII, seguido por Gottfried Leibniz diez años más tarde, con el fin de resolver sistemas de ecuaciones lineales simultáneas utilizando matrices. Entre los siglos XVI y XVII se consolidó la noción de número complejo, con lo cual la noción de álgebra empezaba a apartarse de cantidades medibles. Gabriel Cramer también hizo un trabajo sobre matrices y determinantes en el siglo XVIII. También Leonhard Euler, Joseph-Louis Lagrange, Adrien-Marie Legendre y numerosos matemáticos del siglo XVIII hicieron avances notables en álgebra.

Después de leer esta información nos podemos darnos cuenta que el álgebra no se hizo de un día para otro; como toda ciencia tardo miles de años en llegar a ser lo que hoy conocemos. El proceso fue largo, cada civilización y diferentes matemáticos hicieron aportaciones que llevaron al desarrollo del álgebra actual.

Fuentes de información:

http://www.juntadeandalucia.es/averroes/~29700989/departamentos/departamentos/departamento_de_matemat/recursos/apuntes/histalg.pdf

http://es.slideshare.net/mijinina/historia-del-lgebra

Excel y su entorno.

Hoy día el buen manejo de la tecnología es indispensable, puesto que vivimos en un mundo donde la tecnología y el futuro van tomados de la mano.  Saber manejar adecuadamente las herramientas tecnológicas te abre la posibilidad a un mejor desempeño profesional. Excel es un programa muy utilizado en la actualidad y es utilizado en áreas como: educación, finanzas, producción, administración, entre muchas otras.

¿Qué es Excel?

Es un programa de la suite de office, que está orientado a operaciones matemáticas.

¿Para qué sirve?

Sirve para realizar todo tipo de operaciones  matemáticas, tales como: aritméticas, estadísticas, logarítmicas, contables, gráficos etcétera. Excel  te permite crear y manipular datos; también es una herramienta que te ayuda a automatizar gran parte de tu trabajo.

El entorno de Excel.

Excel se compone de una hoja de cálculo, donde podemos observar filas representadas por números y columnas representadas por letras. La celda es la combinación de una letra con un número.

Al abrir Excel lo primero que observamos es lo siguiente:

 

 Barra de herramientas o cinta de opciones.

Esta barra contiene todas las herramientas que puedes utilizar para editar y manipular los datos que ingresaste en tu hoja de cálculo.

La barra de herramientas o cintilla de opciones de divide en siete menús.

Inicio:

Aquí se encuentran las herramientas más sencillas como el tipo de letra texto, los bordes de las celdas, combinar y centrar celdas etcétera.

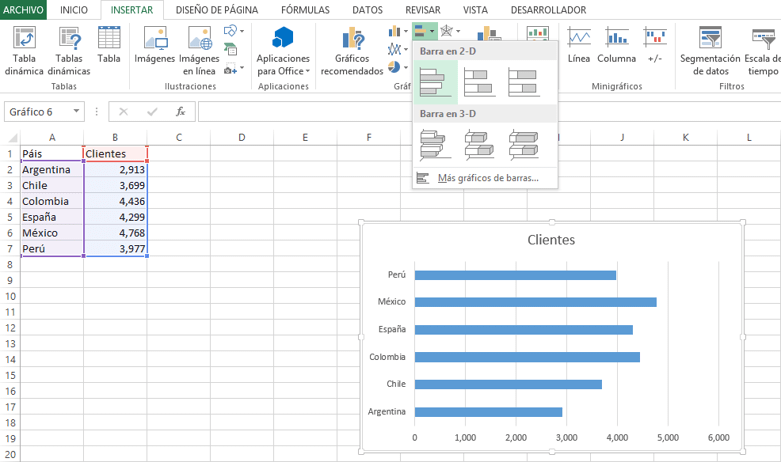
Insertar:

En este menú puedes insertar cualquier elemento a tu hoja de cálculo; por ejemplo: tablas, formas, gráficos, imágenes, ecuaciones entre otras.

Diseño de página:

En esta herramienta puedes editar aspecto tales como: márgenes, orientación de la página, áreas de impresión, fondo etc.

Formulas:

Como ya mencionamos Excel está orientado para realizar operaciones matemáticas. Esta herramienta nos sirve para ingresar una formula a nuestra hoja de cálculo.

Datos:

En esta opción puedes poner las referencias o fuentes de donde tomaste la información.

Revisar:

En la sección de revisar te confirmas que los que hiciste este correctamente.

Vista:

Aquí puedes observar las diferentes vistas de tu trabajo, aplicar zoom, ampliar una sección entre otras.

El siguiente video te explica los elementos más básicos de Excel de una forma sencilla. 

Conceptos Básicos De Álgebra: El memorama como un instrumento de aprendizaje.

C

onocer los conceptos básicos de álgebra, resulta fundamental para comprender el lenguaje algebraico, si comprendemos éste, nos resultará muchos más fácil poder efectuar, las operaciones algebraicas, desde las más sencillas hasta la más complicadas.

Se ha detectado que una gran parte de los estudiantes, desconocen los conceptos fundamentales como: término algebraico, variable, exponente, etcétera y esto dificulta su capacidad para aprender y avanzar en el área de matemáticas.

En el siguiente documento se muestra los conceptos más fundamentales del algebra en un lenguaje sencillo; además te plantea la idea de utilizar un memorama algebraico como herramienta de aprendizaje en la comprensión de los conceptos. Espero que la información te sea de ayuda.

¡Saludos!

Memorama Como Un Instrumento De Aprendizaje. from Elisa Reyes

Ejercicio 2

El siguiente ejercicio es un resumen de los números complejos, sus aplicaciones y el teorema de Möivre. También se incluyen algunas funciones de Excel que sirven para la resolución de problemas relacionados con este teorema.Estos temas los hemos tratado en mis publicaciones anteriores.

No olvides comentar para poder despejar tus dudas y tomar en cuenta tus comentarios, con el fin, de mejorar el blog.

¡Saludos!

Ejercicio 2 contestado from Elisa Reyes

Potencias y Raíces de Números Complejos

Ya hemos tratado este tema en la ocasión anterior,  ya sabemos que un número complejo se representa en la forma binomica z= a+bi. 

Nos resulta sencillo  realizar las operaciones aritméticas utilizando los números complejos; pero al extraer su raíz o elevar este número complejo una potencia aún quedan dudas  y nos puede parecer una tarea sumamente complicada, con el fin de despejar tus dudas, te dejo aquí abajo un video explicando las potencias y raíces de los números complejos. Espero que el material te sea de ayuda.

No olvides dejar un comentario acerca del video, las dudas que tengas, una opinión etcétera.

¡Saludos!

Potencias y Raíces de números complejos

Realizar operaciones con números complejos, es muy diferente a las operaciones usuales y se requiere de los conocimientos de álgebra y trigonometría para poder resolverlos.

En el siguiente archivo se muestra la forma de representar los números complejos mediante el plano complejo, convertir estos números a su forma polar y trigonométrica, la forma en cómo elevarlos a una potencia y cómo extraerles su raíz.

Complex numbers powers and roots from Edgar Mata

A continuación se muestra otro archivo ya contestado ejemplificando todos los temas referentes a los números complejos.

Actividad 3 contestada from Elisa Reyes