Los números irracionales y sus propiedades

¿Qué es un número irracional?

Un número irracional es aquel que no puede ser expresado como una fracción m/n puesto  que poseen infinitas cifras decimales no periódicas, que por lo tanto no pueden ser expresados como fracciones. En un principio se les llamaba inconmensurables, debido a la gran cantidad de cifras que contienen.

Ejemplo: Pi es un número irracional. El valor de Pi es

3,1415926535897932384626433832795 (y más...)

Los decimales no siguen ningún patrón, y no se puede escribir ninguna fracción que tenga el valor Pi.

¿Cómo se descubrieron los números irracionales?

El problema se les presentó cuando trataron de medir la hipotenusa de un triángulo rectángulo isósceles que se les formaba en una baldosa cuadrada dividida en dos partes 

por una de sus diagonales.

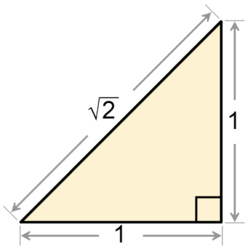
Tomando como unidad el cateto de este triángulo y aplicando el Teorema de Pitágoras, apareció el primer número irracional que es:

(√2) cuyo valor aproximado es 1,4142135...

Propiedades de los números irracionales.

Además de ser un número infinito decimal no periódico, los números irracionales tienen otras propiedades como:

- Propiedad conmutativa: en la suma y la multiplicación se cumple la propiedad conmutativa según la cual el orden de los factores no altera el resultado, por ejemplo, π+ϕ = ϕ+π; así como en la multiplicación, π×ϕ=ϕ×π.

- Propiedad asociativa: donde la distribución y agrupación de los números da como resultado el mismo número, de manera independiente a su agrupación, siendo (ϕ+π)+e=ϕ+ (π+e); y de la misma manera con la multiplicación, (ϕ×π) ×e=ϕ× (π×e).

- Elemento opuesto: existe un inverso aditivo, para la suma de números irracionales, es decir que para cada número tiene su negativo que lo anula, por ejemplo π-π=0 y de la misma forma un inverso multiplicativo que da como resultado 1, es decir ϕ×1/ ϕ = 1.

- La multiplicación es distributiva en relación a la suma y a la resta.

Ejemplo: (3+2) π =3π+2π=5π.

- Propiedad cerrada: es decir que el resultado de la suma, resta, multiplicación, división o potenciación de un número irracional, siempre será un número irracional. Sin embargo, la propiedad cerrada no se cumple en el caso de la radicación.